A. Pengertian Koefisien, Variabel, Konstanta, Dan Suku
Di kelas VII Anda sudah mempelajari mengenai bentuk-bentuk aljabar.
Selain itu, Anda juga harus menguasai materi tentang KPK dari dua
bilangan atau lebih dan sifat-sifat operasi hitung pada bilangan bulat.
Perhatikan uraian berikut. Bonar dan Cut Mimi membeli alat-alat tulis di
koperasi sekolah. Mereka membeli 5 buku tulis, 2 pensil, dan 3 bolpoin.
Jika buku tulis dinyatakan dengan x, pensil dengan y, dan bolpoin
dengan z maka Bonar dan Cut Mimi membeli
5x + 2y + 3z.
Selanjutnya, bentuk-bentuk
5x + 2y + 3z, 2x2, 4xy2, 5x2 – 1 dan (x – 1) (x + 3)
disebut bentuk-bentuk aljabar. Sebelum mempelajari faktorisasi suku aljabar, marilah kita ingat kembali istilah-istilah yang terdapat pada bentuk aljabar.
Baca Juga:
Baca Juga:
- Variabel
Variabel adalah lambang pengganti suatu bilangan yang belum diketahui
nilainya dengan jelas. Variabel disebut juga peubah. Variabel biasanya
dilambangkan dengan huruf kecil a, b, c, … z.
Contoh Soal
Tulislah setiap kalimat “Suatu bilangan jika dikalikan 5 kemudian
dikurangi 3, hasilnya adalah 12” dengan menggunakan variabel sebagai
pengganti bilangan yang belum diketahui nilainya.
Penyelesaian:
Misalkan bilangan tersebut x, berarti
5x – 3 = 12.
- Konstanta
Suku dari suatu bentuk aljabar yang berupa bilangan dan tidak memuat variabel disebut konstanta.
Contoh Soal
Tentukan konstanta pada bentuk aljabar
2x2 + 3xy + 7x – y – 8
Penyelesaian:
Konstanta adalah suku yang tidak memuat variabel, sehingga konstanta dari
2x2 + 3xy + 7x – y – 8 adalah –8.
- Koefisien
Koefisien pada bentuk aljabar adalah faktor konstanta dari suatu suku pada bentuk aljabar.
Contoh Soal
Tentukan koefisien x pada bentuk aljabar
2x2 + 6x – 3
Penyelesaian:
Koefisien x dari 2x2 + 6x – 3 adalah 6.
- Suku
Suku adalah variabel beserta koefisiennya atau konstanta pada bentuk aljabar yang dipisahkan oleh operasi jumlah atau selisih.
a. Suku satu adalah bentuk aljabar yang tidak dihubungkan oleh operasi jumlah atau selisih.
Contoh: 3x, 4a2, –2ab, …
b. Suku dua adalah bentuk aljabar yang dihubungkan oleh satu operasi jumlah atau selisih.
Contoh: a2 + 2, x + 2y, 3×2 – 5x, …
c. Suku tiga adalah bentuk aljabar yang dihubungkan oleh dua operasi jumlah atau selisih.
Contoh: 3×2 + 4x – 5, 2x + 2y – xy, …
Bentuk aljabar yang mempunyai lebih dari dua suku disebut suku banyak atau polinom.
B. Penjumlahan dan Pengurangan Bentuk Aljabar
Untuk memudahkan Anda memahami konsep penjumlahan dan pengurangan bentuk aljabar perhatikan uraian berikut ini “Wawan memiliki 10 kelereng merah dan 4 kelereng putih. Jika kelereng merah dinyatakan dengan x dan kelereng putih dinyatakan dengan y maka banyaknya kelereng Wawan adalah 10x + 4y”. Selanjutnya, “jika Wawan diberi kakaknya 7 kelereng merah dan 3 kelereng putih maka banyaknya kelereng Wawan sekarang adalah 17x + 7y”. Hasil ini diperoleh dari
(10x + 4y) + (7x + 3y).
Amatilah bentuk aljabar
3x2 – 2x + 3y + x2 + 5x + 10
Suku-suku 3x2 dan x2 disebut suku-suku sejenis, demikian juga suku-suku –2x dan 5x. Adapun suku-suku –2x dan 3y merupakan suku-suku tidak sejenis.
Suku-suku sejenis adalah suku yang memiliki variabel dan pangkat dari
masing-masing variabel yang sama. Pemahaman mengenai suku-suku sejenis
dan suku-suku tidak sejenis sangat bermanfaat dalam menyelesaikan
operasi penjumlahan dan pengurangan dari bentuk aljabar. Operasi
penjumlahan dan pengurangan pada bentuk aljabar dapat diselesaikan
dengan memanfaatkan sifat komutatif, asosiatif, dan distributif dengan
memerhatikan suku-suku yang sejenis. Sifat-sifat tersebut berlaku pada
penjumlahan dan pengurangan bentuk aljabar.
Contoh Soal 1
Tentukan hasil penjumlahan
3x2 – 2x + 5 dengan x2 + 4x – 3
Penyelesaian:
(3x2 – 2x + 5) + (x2 + 4x – 3)
= 3x2 – 2x + 5 + x2 + 4x – 3
= 3x2 + x2 – 2x + 4x + 5 – 3 (kelompokkan suku-suku sejenis)
= (3 + 1)x2 + (–2 + 4)x + (5 – 3) (sifat distributif)
= 4x2 + 2x + 2
Contoh Soal 2
Tentukan hasil pengurangan
4y2 – 3y + 2 dari 2(5y2 – 3)
Penyelesaian:
2(5y2 – 3) – (4y2 – 3y + 2)
= 10y2 – 6 – 4y2 + 3y – 2
= (10 – 4)y2 + 3y + (–6 – 2)
= 6y2 + 3y – 8
C.Penjumlahan dan pengurangan pecahan aljabar
Adapun pada penjumlahan dan pengurangan pecahan aljabar dengan penyebut berbeda dapat dilakukan dengan cara menyamakan penyebutnya terlebih dahulu menjadi kelipatan persekutuan terkecil (KPK) dari penyebut-penyebutnya.
Contoh Soal 1
Contoh soal 2
D. Contoh soal penjumlahan dan pengurangan bentuk aljabar
Konsep dasar yang harus anda kuasai jika ingin memahami konsep penjumlahan danpengurangan bentuk aljabar adalah
suku-suku sejenis. Apa itu suku-suku sejenis? Tetapi sebelum Anda
mempelajari tentang suku-suku sejenis Anda terlebih dahulu harus
memahami apa itu suku. Untuk memahami konsep itu silahkan anda baca
tentangkonsep variabel, konstanta, koefiseien dan suku.
Sekarang perhatikan uraian berikut ini untuk memahami konsep penjumlahan dan pengurangan aljabar.
Budi memiliki 16 kelereng hijau dan 7 kelereng biru. Jika kelereng
hijau dinyatakan dengan x dan kelereng biru dinyatakan dengan y maka
banyaknya kelereng Budi adalah 16x + 7y. Selanjutnya, jika Budi diberi
kakaknya 5 kelereng hijau dan 12 kelereng biru maka banyaknya kelereng
Budi sekarang adalah 21x + 19y. Hasil ini diperoleh dari (16x + 7y) +
(5x + 12y).
Amatilah bentuk aljabar
3x2 – 2x + 3y + x2 + 5x + 10
Suku-suku 3x2 dan x2 disebut
suku-suku sejenis, demikian juga suku-suku –2x dan 5x. Adapun suku-suku
–2x dan 3y merupakan suku-suku tidak sejenis. begitu juga dengan
suku-suku 3x2 dan x2 merupakan suku-suku tidak sejenis.
Jadi pengertian suku-suku sejenis adalah suku yang memiliki variabel dan pangkat dari masing-masing variabel yang sama.
Pemahaman mengenai suku-suku sejenis dan suku-suku tidak sejenis
sangat bermanfaat dalam menyelesaikan operasi penjumlahan dan
pengurangan dari bentuk aljabar. Operasi penjumlahan dan pengurangan
pada bentuk aljabar dapat diselesaikan dengan memanfaatkan sifat
komutatif, asosiatif, dan distributif dengan memerhatikan suku-suku yang
sejenis. Sifat-sifat tersebut berlaku pada penjumlahan dan pengurangan
bentuk aljabar.
Contoh soal 1
Sederhanakan bentuk-bentuk aljabar berikut.
a. (2x + 8) + (4x – 5 – 5y)
b. (3p + q) + (–2p – 5q + 7)
c. (3x2 + 2x – 1) + (x2 – 5x + 6)
d. 2(x + 2y – xy) + 5(2x – 3y + 5xy)
Jawab:
a. kumpulkan suku-suku sejenis terlebih dahulu
(2x + 8) + (4x – 5 – 5y)
= 2x+4x – 5y +8 – 5
= 6x – 5y 3
b. kumpulkan suku-suku sejenis terlebih dahulu
(3p + q) + (–2p – 5q + 7)
= 3p – 2p +q – 5q + 7
= p – 4q + 7
c. kumpulkan suku-suku sejenis terlebih dahulu
(3x2 + 2x – 1) + (x2 – 5x + 6)
= (3x2 + x2) + (2x – 5x) +(– 1 + 6)
= 4x2 – 3x +5
d. Jabarkan terlebih dahulu baru kemudian jumlahkan suku-suku yang sejenis
2(x + 2y – xy) + 5(2x – 3y + 5xy)
= (2x + 4y – 2xy) + (10x – 15y + 25xy)
= (2x + 10x) + (4y – 15y) + (-2xy +25xy)
= 12x – 11y + 23xy
Contoh soal 2
Sederhanakan bentuk-bentuk aljabar berikut.
a. (2x + 5) – (x – 3)
b. (x2 + 4x – 1) – (2x2 + 4x)
c. (y2 – 3) – (4y2 + 5y + 6)
d. (5a – 6 + ab) – (a + 2ab – 1)
Jawab:
a. Jabarkan terlebih dahulu baru kemudian kumpulkan suku-suku yang sejenis
(2x + 5) – (x – 3)
= 2x + 5 –x +3
= 2x – x +5 +3
= x +8
b. Jabarkan terlebih dahulu baru kemudian kumpulkan suku-suku yang sejenis
(x2 + 4x – 1) – (2x2 + 4x)
= x2 + 4x – 1 – 2x2 – 4x
= x2 – 2x2 + 4x – 4x – 1
= –x2 – 1
c. Jabarkan terlebih dahulu baru kemudian kumpulkan suku-suku yang sejenis
(y2 – 3) – (4y2 + 5y + 6)
= y2 – 3 – 4y2 – 5y – 6
= y2 – 4y2 – 5y – 3 – 6
= –3y2 – 5y – 9
d. Jabarkan terlebih dahulu baru kemudian kumpulkan suku-suku yang sejenis
(5a – 6 + ab) – (a + 2ab – 1)
= 5a – 6 + ab – a – 2ab + 1
= 5a – a + ab – 2ab – 6 + 1
= 4a – ab – 5
Contoh Soal 3
Sederhanakan bentuk-bentuk aljabar berikut.
a. a2 + 2ab – 3b2 – 7a2 – 5ab
b. x2 – x – 6 + 3x2 – xy
c. 3p3 – 2pq2 + p2q – 7p3 + 2p2q
d. –2(p3 – 2pq + q2) + 3(p3 + 4pq –q2)
Jawab:
a. Kumpulkan suku-suku yang sejenis
a2 + 2ab – 3b2 – 7a2 – 5ab
= (a2 – 7a2) + (2ab – 5ab) – 3b2
= – 6a2 – 3ab – 3b2
b. Kumpulkan suku-suku yang sejenis
x2 – x – 6 + 3x2 – xy
= (x2 + 3x2) – x – xy – 6
= 4x2 – x – xy – 6
c. Kumpulkan suku-suku yang sejenis
3p3 – 2pq2 + p2q – 7p3 + 2p2q
= (3p3 – 7p3) + (p2q + 2p2q) – 2pq2
= – 4p3 + 3p2q – 2pq2
d. Jabarkan terlebih dahulu baru kemudian kumpulkan suku-suku yang sejenis
–2(p3 – 2pq + q2) + 3(p3 + 4pq –q2)
= –2p3 + 4pq – 2q2 + 3p3 + 12pq – 3q2
= (–2p3 + 3p3) + (– 2q2 – 3q2) + (4pq + 12pq)
= p3 – 5q2 + 16pq
E.Perkalian suatu bilangan dengan bentuk aljabar
Sebelumnya kita sudah membahas penjumlahan dan pengurangan bentuk
aljabar dan juga contoh soal penjumlahan dan pengurangan bentuk aljabar. kali ini akan membahas perkalian bentuk aljabar yaitu perkalian suatu bilangan dengan bentuk aljabar.
- Perkalian suatu bilangan dengan bentuk aljabar
Coba kalian ingat kembali sifat distributif pada bilangan bulat. Jika a, b, dan c bilangan bulat maka berlaku a(b + c) = ab +
ac. Sifat distributif ini dapat dimanfaatkan untuk menyelesaikan
operasi perkalian pada bentuk aljabar. Perkalian suku dua (ax + b)
dengan skalar/bilangan k dinyatakan sebagai berikut.
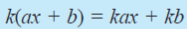
Sebagai contoh berikut hasil penjabaran bentuk perkalian 2(3x – y) yakni:
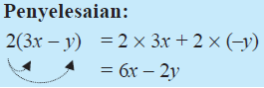
Contoh soal 1
Tentukan hasil perkalian bentuk aljabar berikut
a. 2(x + 4)
b. –3(a – 2b)
c. 5(3x + 2y)
d. –2a(a + 4b)
Penyelesaian:
a. 2(x + 4) = 2x + 8
b. –3(a – 2b) = –3a + 6b
c. 5(3x + 2y) = 15x + 10y
d. –2a(a + 4b) = –2a2 – 8ab
Contoh soal 2
Tentukan hasil perkalian bentuk aljabar berikut
a. 4a2(–a + 2b)
b. 2xy(x – 4)
c. –p2(p2 – 3p)
d. ½ (4x – 6y)
Penyelesaian:
a. 4a2(–a + 2b) = –4a3 + 8a2b)
b. 2xy(x – 4) = 2x2y – 8xy
c. –p2(p2 – 3p) = –p4 +3p3
d. ½ (4x – 6y) = 2x – 3y
Contoh soal 3
Tentukan hasil perkalian bentuk aljabar berikut
a. 5x(8y – 9z)
b. 8y(5x – 9z)
c. 4x (x – 2y)
d. 8a (3ab – 2ab2 – 8ab)
e. 7(2x + 5)
f. (3x – 7) 4x
Penyelesaian:
a. 5x(8y – 9z) = 40xy – 45xz
b. 8y(5x – 9z) = 40xy – 72yz
c. 4x (x – 2y) = 4x2 – 8xy
d. 8a (3ab – 2ab2 – 8ab) = 24a2b – 16a2b2 – 64a2b
e. 7(2x + 5) = 14x + 35
f. (3x – 7) 4x = 12x2 – 28x
F.Perkalian antara bentuk aljabar dengan bentuk aljabar
Telah kalian pelajari bahwa perkalian antara bilanganskalar k
dengan suku dua (ax + b) adalah k (ax + b) = kax + kb. Dengan
memanfaatkan sifat distributif pula, perkalian antara bentuk aljabar
suku dua (ax + b) dengan suku dua (ax + d) diperoleh sebagai berikut.
(ax + b) (cx + d)
= ax(cx + d) + b(cx + d)
= ax(cx) + ax(d) + b(cx) + bd
= acx2 + (ad + bc)x + bd
Sifat distributif dapat pula digunakan pada perkalian suku dua dan suku tiga.

Selanjutnya, kita akan membahas mengenai hasil perkalian (ax + b) (ax + b), (ax + b)(ax – b), (ax – b)(ax – b), dan (ax +b) (ax2 + bx + c). Pelajari uraian berikut ini.
a. (ax+b)2
= (ax+b) (ax+b)
= ax (ax+b) + b (ax+b)
= ax(ax) + ax(b) + b(ax) +b2
= a2x2 +abx + abx +b2
= a2x2 +2abx +b2
b. (ax + b)(ax – b)
= ax (ax – b) + b(ax – b)
= ax(ax) – ax(b) + b(ax) +b(–b)
= a2x2 – abx – abx –b2
= a2x2 – b2
c. (ax – b)(ax – b)
= ax (ax – b) – b(ax – b)
= ax(ax) – ax(b) – b(ax) –b(–b)
= a2x2 – abx – abx +b2
= a2x2 – 2abx + b2
d. (ax+b)(ax2 + bx + c)
= (ax + b) (ax2 + bx + c)
= ax (ax2 + bx + c) + b (ax2 + bx + c)
= ax(ax2) + ax(bx) + ax(c) + b(ax2) + b(bx) + b(c)
= a2x3 + abx2 + abx2 + b2x + bc
= a2x3 + 2abx2 + b2x + bc
Berikut contoh soal dan cara pengerjaan hasil perkalian bentuk aljabar dari (x + 2)(x + 3) adalah:
Cara 1 dengan sifat distributif
(x + 2)(x + 3)
= x (x + 3) + 2(x + 3)
= x2 + 3x + 2x + 3
= x2 + 5x + 3
Cara 2 dengan skema
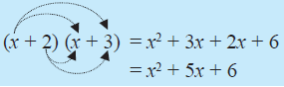
Contoh soal yang lain lagi yakni hasil dari perkalian (2x + 3)(x2 + 2x – 5) yakni:
Cara 1 dengan sifat distributif
(2x + 3)(x2 + 2x – 5)
= 2x(x2 + 2x – 5) + 3(x2 + 2x – 5)
= 4x3 + 4x2 – 10x + 3x2 + 6x – 15
= 4x3 + 7x2 – 4x – 15
Cara 2 dengan skema
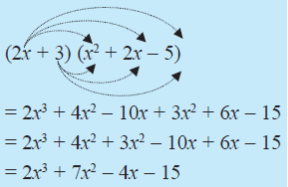
Contoh Soal 1
Jabarkan bentuk perkalian berikut!
a. (2x – 3) (x + 5)
b. (3x – y) (x + y)
c. (5m – 1) (m + 4)
d. (2p + q) (p – 4q)
e. (a – 4) (2a + 3)
Penyelesaian:
a. Dengan menggunakan cara distributif
(2x – 3) (x + 5)
= 2x (x + 5) – (x + 5)
= 2x (x) + 2x(5) – x – 5
= 2x2 + 10x – x – 5
= 2x2 + 9x – 5
b. Dengan menggunakan cara distributif
(3x – y) (x + y)
= 3x(x + y) – y(x + y)
= 3x2 + 3xy – yx – y2
= 3x2 + 2xy – y2
c. Dengan menggunakan cara distributif
(5m – 1) (m + 4)
= 5m(m + 4) – 1(m + 4)
= 5m2 +4m – m – 4
= 5m2 + 3m – 4
d. Dengan menggunakan cara distributif
(2p + q) (p – 4q)
= 2p(p – 4q) + q(p – 4q)
= 2p2 – 8pq + qp – 4q2
= 2p2 – 7pq – 4q2
e. Dengan menggunakan cara distributif
(a – 4) (2a + 3)
= a(2a + 3) – 4(2a + 3)
= 2a2 +3a – 8a – 12
= 2a2 – 5a – 12
Contoh Soal 2
Jabarkan bentuk perkalian berikut
a. (2x + 3) (x – 4)
b. (a + 3b) (a – 5b)
c. (5m – 1) (2m + 4)
d. (a – 3) (a2 + 4a + 5)
e. (x + y) (3x2 + xy + 2y2)
Penyelesaian:
a. Dengan menggunakan cara distributif
(2x + 3) (x – 4)
= 2x(x – 4) + 3(x – 4)
= 2x2 – 8x + 3x – 12
= 2x2 – 5x – 12
b. Dengan menggunakan cara distributif
(a + 3b) (a – 5b)
= a(a – 5b) + 3b(a – 5b)
= a2 – 5ab + 3ab – 15b2
= a2 – 2ab – 15b2
c. Dengan menggunakan cara distributif
(5m – 1) (2m + 4)
= 5m(2m + 4) – 1(2m + 4)
= 10m2 +20m – 2m – 4
= 10m2 + 18m – 4
d. Dengan menggunakan cara distributif
(a – 3) (a2 + 4a + 5)
= a(a2 + 4a + 5) – 3(a2 + 4a + 5)
= a3 + 4a2 +5a – 3a2 – 12a – 15
= a3 + a2 – 7a – 15
e. Dengan menggunakan cara distributif
(x + y) (3x2 + xy + 2y2)
= x(3x2 + xy + 2y2) + y(3x2 + xy + 2y2)
= 3x3 +x2y + 2xy2 + 3x2y + xy2 + 2y3
= 3x3 + 4x2y + 3xy2 + 2y3
Contoh Soal 3
Tentukan hasil perkalian berikut
a. ab(a + 2b – c)
b. 5xy(x – 3y + 5)
c. 2xy(x – 3y)
d. 5a(3ab – 2ac)
e. 3y(4xy – 4yz)
Penyelesaian:
a. ab(a + 2b – c) = a2b + 2ab2 – abc
b. 5xy(x – 3y + 5) = 5x2y – 15xy2 + 25xy
c. 2xy(x – 3y) = 2x2y – 6xy2
d. 5a(3ab – 2ac) = 15a2b – 10a2c
e. 3y(4xy – 4yz) = 12xy2 – 12y2z
G. Pembagian bentuk aljabar
Suatu bilangan a dapat diubah menjadi a = p x qdengan a, p, q bilangan bulat maka p dan q disebutfaktor-faktor dari a. Hal tersebut berlaku pula pada bentuk aljabar. Perhatikan uraian berikut.
3x3yz2 = 3. x3 . y . z2
x2y3z = x2.y3.z
Pada bentuk aljabar di atas, 3, x3, y, dan z2 adalah faktor-faktor dari 3x3yz2, sedangkan x2, y3, dan zadalah faktor-faktor dari bentuk aljabar x2y3z. Faktor sekutu (faktor yang sama) dari 3x3yz2 dan x2y3zadalah x2, y, dan z, sehingga diperoleh
3x3yz2/ x2y3z = x2yz (3xz)/ x2yz (y2) = 3xz/y2
Berdasarkan uraian di atas dapat kita simpulkan
bahwa jika dua bentuk aljabar memiliki faktor sekutu yang sama maka
hasil bagi kedua bentuk aljabar tersebut dapat ditulis dalam bentuk yang
lebih sederhana. Dengan demikian, pada operasi pembagian bentuk aljabar
Anda harus menentukan terlebih dahulu faktor sekutu kedua bentuk
aljabar tersebut, kemudian baru dilakukan pembagian. Untuk memantapkan
pemahaman anda tentang pembagian dalam bentuk aljabar silahkan
perhatikan contoh soal berikut ini.
Contoh Soal
Tentukan hasil pembagian dari bentuk aljabar berikut ini.
1. 6xy : 2y
2. 10a2b4c3 : 2abc
3. p4q6r5 : pq2r3
4. 6x3y7 : 2xy : 3y
5. 18a3b5c6 : 2ab2 : 3a2c2
6. 20a4b5c7 : (4a2b2c3 : 2abc)
7. 21p4q5r3 : (8p2qr3 : 2pqr)
8. 3x2y × 2yz2 : xyz
9. 30x6y9 : (5x4y2 × 2xy3)
10. 32x4yz6 : 2xyz × 4xy2z3
Penyelesaian:
1. Faktor sekutu (faktor yang sama) dari 6xy dan 2y adalah 2, dan y, sehingga diperoleh:
6xy : 2y = 2y(3x)/2y(1) = 3x
2. Faktor sekutu (faktor yang sama) dari 10a2b4c3 dan 2abc adalah 2, a, b dan c, sehingga diperoleh:
10a2b4c3 : 2abc
= 10a2b4c3/2abc
= 2abc (5ab3c2)/2abc
= 5ab3c2
3. Faktor sekutu (faktor yang sama) dari p4q6r5 dan pq2r3 adalah p, q2, dan r3, sehingga diperoleh:
p4q6r5 : pq2r3
= p4q6r5/pq2r3
= pq2r3 (p3q4r2)/pq2r3
= p3q4r2
4. Kerjakan terlebih dahulu 6x3y7 : 2xy, faktor sekutu (faktor yang sama) dari 6x3y7 dan 2xy adalah 2, x, dan y, sehingga diperoleh
6x3y7 : 2xy
= 2xy (3x2y6)/2xy
= 3x2y6
kemudian hasil 3x2y6 dibagi dengan 3y, faktor sekutu (faktor yang sama) dari 3x2y6 dan 3y adalah 3 dan y, sehingga diperoleh:
3x2y6/3y = 3y(x2y5)/3y = x2y5
Jadi 6x3y7 : 2xy : 3y = x2y5
5. Kerjakan terlebih dahulu 18a3b5c6 : 2ab2, faktor sekutu (faktor yang sama) dari 18a3b5c6 dan 2ab2adalah 2, a, dan b2, sehingga diperoleh
18a3b5c6 : 2ab2
= 2ab2(9a2b3c6)/ 2ab2
= 9a2b3c6
kemudian hasil 9a2b3c6 dibagi dengan 3a2c2, faktor sekutu (faktor yang sama) dari 9a2b3c6 dan 3a2c2adalah 3, a2 dan c2, sehingga diperoleh:
9a2b3c6: 3a2c2
= 3a2c2(3b3c4)/3a2c2
= 3b3c
Jadi 18a3b5c6 : 2ab2 : 3a2c2 = 3b3c4
6. Kerjakan terlebih dahulu yang ada di dalam kurung yaitu (4a2b2c3 : 2abc), faktor sekutu (faktor yang sama) dari 4a2b2c3 dan 2abc adalah 2, a, b, dan c, sehingga diperoleh
4a2b2c3 : 2abc
= 2abc (2abc2)/ 2abc
= 2abc2
kemudian 20a4b5c7 dibagi dengan hasil 2abc2, faktor sekutu (faktor yang sama) dari 20a4b5c7 dan 2abc2adalah 2, a, b, dan c2, sehingga diperoleh:
20a4b5c7 : 2abc2
= 2abc2 (10a3b4c5)/ 2abc2
= 10a3b4c5
Jadi 20a4b5c7 : (4a2b2c3 : 2abc) = 10a3b4c5
7. Kerjakan terlebih dahulu yang ada di dalam kurung yaitu (8p2qr3 : 2pqr), faktor sekutu (faktor yang sama) dari 8p2qr3 dan 2pqr adalah 2, p, q, dan r, sehingga diperoleh
8p2qr3 : 2pqr
= 2pqr (4pr2)/ 2pqr
= 4pr2
kemudian 21p4q5r3 dibagi dengan hasil 4pr2, faktor sekutu (faktor yang sama) dari 21p4q5r3 dan 4pr2adalah p, dan r2, sehingga diperoleh:
21p4q5r3 : 4pr2
= pr2 (21p3q5r)/ pr2(4)
= 21p3q5r/4
Jadi 21p4q5r3 : (8p2qr3 : 2pqr) = 21p3q5r/4
8. Sama seperti soal-soal sebelumnya hanya saja Anda bisa memilih
yang mana anda kerjakan terlebih dahulu (saya pilih pembagian terlebih
dahulu),
3x2y × (2yz2 : xyz)
= 3x2y × (2z/x)
= 3xy/2z
9. Sama seperti soal-soal sebelumnya hanya saja Anda bisa memilih
yang mana anda kerjakan terlebih dahulu (saya pilih yang di dalam kurung
terlebih dahulu),
30x6y9 : (5x4y2 × 2xy3)
= 30x6y9 : 10x5y5
= 3xy4
10. Sama seperti soal-soal sebelumnya hanya saja Anda bisa memilih
yang mana anda kerjakan terlebih dahulu (saya pilih pembagian terlebih
dahulu)
(32x4yz6 : 2xyz) × 4xy2z3
= 16x3z5 × 4xy2z3
= 64x4y2z8
H.Pemfaktoran aljabar dalam bentuk ax + bx – cx
Proses menyatakan bentuk penjumlahan menjadi suatu bentuk perkalian faktor-faktornya
disebut pemfaktoran atau faktorisasi. Pemfaktoran atau faktorisasi
bentuk aljabar adalah menyatakan bentuk penjumlahan menjadi suatu bentuk
perkalian dari bentuk aljabar tersebut.
Sekarang, Mafia Online akan membahas faktorisasi bentuk ax + ay + az + … dan ax + bx – cx. Bentuk aljabar yang terdiri atas dua suku atau lebih dan memiliki faktor sekutu dapat difaktorkan dengan menggunakan sifat distributif, seperti berikut ini.
ax + ay + az + … = a(x + y + z + …)
ax + bx – cx = x(a + b – c)
Contoh Soal
Faktorkanlah bentuk-bentuk aljabar berikut.
1. 3x – 3y
2. 2x + 6
3. ab + bc
4. x3 + xy2
5. 8pq + 24pqr
4. ap2 + 2ap
5. 4x2y – 6xy3
6. 15x2 – 18xy + 9xz
Penyelesaian:
1. 3x – 3y = 3(x – y)
2. 2x + 6 = 2(x + 3)
3. ab + bc = a(b + c)
4. x3 + xy2 = x (x2 + y2)
5. 8pq + 24pqr = 8pq(1 + 3r)
4. ap2 + 2ap = ap(p+2)
5. 4x2y – 6xy3 = 2xy(2x – 3y2)
6. 15x2 – 18xy + 9xz = 3x(5x – 6y + 3z)
I. Pemfaktoran aljabar selisih dua kuadrat
Bentuk aljabar yang terdiri atas dua suku dan merupakan selisih dua kuadrat dapat dijabarkan sebagai berikut.
x2 – y2
= x2 + (xy – xy) – y2
= (x2 + xy) – (xy + y2)
= x (x +y) – y(x + y)
= (x + y)(x – y)
Dengan demikian, bentuk selisih dua kuadrat x2 – y2dapat dinyatakan sebagai berikut.
x2 – y2 = (x + y)(x – y)
Contoh Soal
Faktorkanlah bentuk-bentuk aljabar berikut
1. 3p2 – 12
2. x2 – 25
3. 64a2 – 9
4. 9m2 – 16
5. 8a2 – 2b2
6. 1 – x2
7. 25p2 – 16q2
8. 49 – p2
9. 36x2 – 81y2
10. 9x2 – 16
11. 81p2 – 100q2
Penyelesaian:
1. 3p2 – 12
= 3(p2 – 4)
= 3 (p – 2)(p + 2)
2. x2 – 25
= x2 – (5)2
= (x + 5)(x – 5)
3. 64a2 – 9
= (8a)2 – (3)2
= (8a + 3)(8a – 3)
4. 9m2 – 16
= (3m)2 – (4)2
= (3m + 4)(3m – 4)
5. 8a2 – 2b2
= 2((8a)2 – b2)
= 2(8a + b)( 8a – b)
6. 1 – x2
= (1 + x)( 1 – x)
7. 25p2 – 16q2
= (5p)2 – (4q)2
= (5p + 4q)(5p – 4q)
8. 49 – p2
= 72 – p2
= (7 + p)(7 – p)
9. 36x2 – 81y2
= (6x)2 – (9y)2
= (6x + 9y)(6x – 9y)
10. 9x2 – 16
= (3x)2 – 42
= (3x + 4)(3x – 4)
11. 81p2 – 100q2
= (9p)2 – (10q)2
= (9p + 10q)(9p – 10q)
BeSmart
-Semoga Bermanfaat-

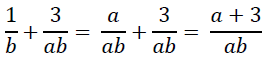
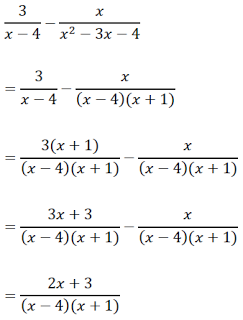
Tidak ada komentar:
Posting Komentar